Figure 10-28.--How a differential works.

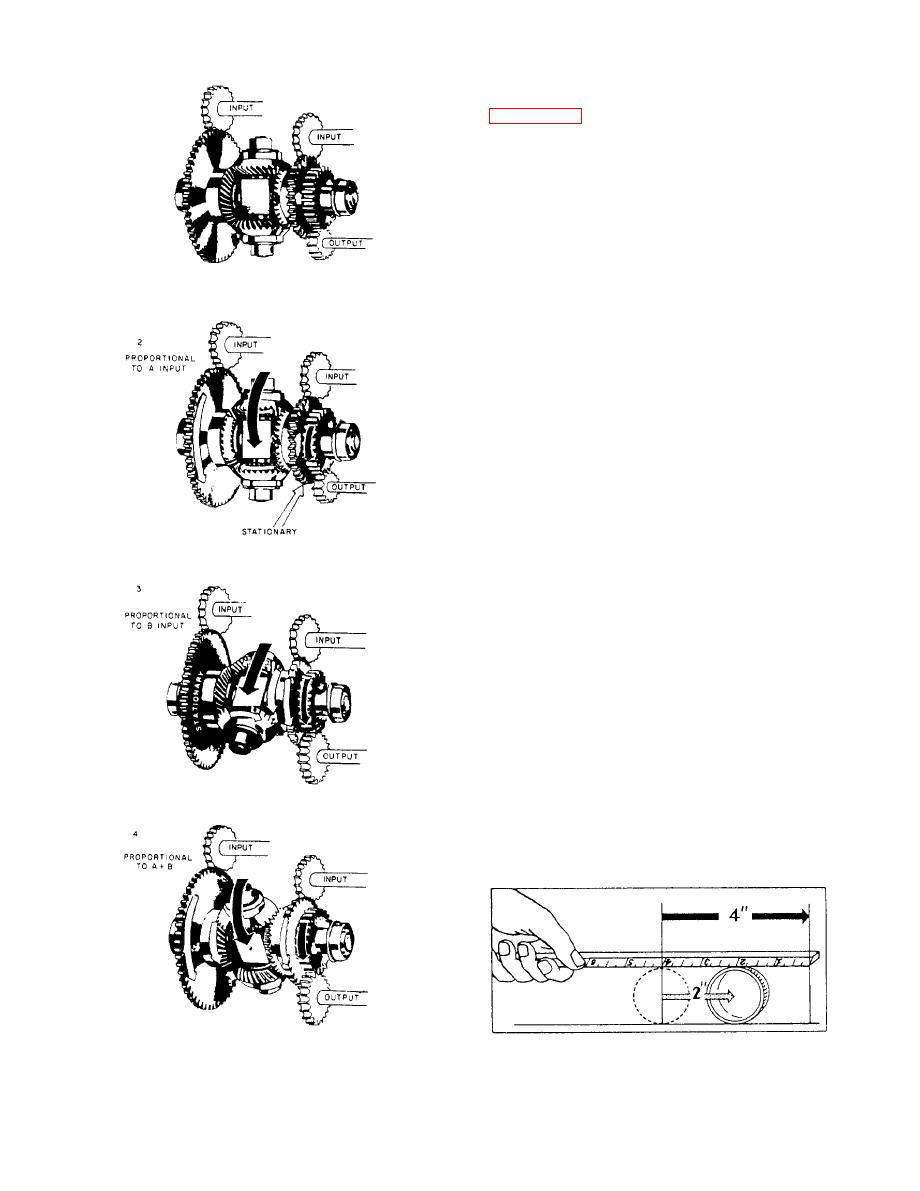as many revolutions as the sum of the revolutions of

the end gears, because the spider gears are free to roll

between the end gears. To understand this better, look

at figure 10-29. Here a cylindrical drinking glass is

rolled along a table top by pushing a ruler across its

upper side. The glass will roll only half as far as the

ruler travels. The spider gears in the differential roll

against the end gears in exactly the same way. Of

course, the answer can be corrected by using a 2:1 gear

ratio between the gear on the spider shaft and the gear

for the output shaft. Very often, for design purposes,

this gear ratio will be found to be different.

When the two sides of the differential move in

opposite directions, the output of the spider shaft is

proportional to the difference of the revolutions of the

two inputs. This is because the spider gears are free to

turn and are driven in opposite directions by the two

inputs. If the two inputs are equal and opposite, the

spider gears will turn, but there will be no movement

of the spider shaft. If the two inputs turn in opposite

directions for an unequal number of revolutions, the

spider gears roll on the end gear that makes the lesser

number of revolutions, rotating the spider in the

direction of the input making the greater number of

revolutions. The motion of the spider shaft will be

equal to half the difference between the revolutions of

the two inputs. A change in the gear ratio to the output

shaft can then give us any proportional answer we

wish.

We have thus far been describing a hookup

wherein the two sides are inputs and the spider shaft

the output, as long as it is recognized that the spider

follows the end gears for half the sum, or difference,

of their revolutions. However, it is not necessary to

always use this type of hookup. The spider shaft may

be used as one input and either of the sides used as the

other. The other side will then become the output. This

fact permits three different hookups for any given

Figure 10-28.--How a differential works.

Figure 10-29.--The spider makes only half as many

revolutions.

10-15