Figure 10-26.--Exploded view of a differential gear system.

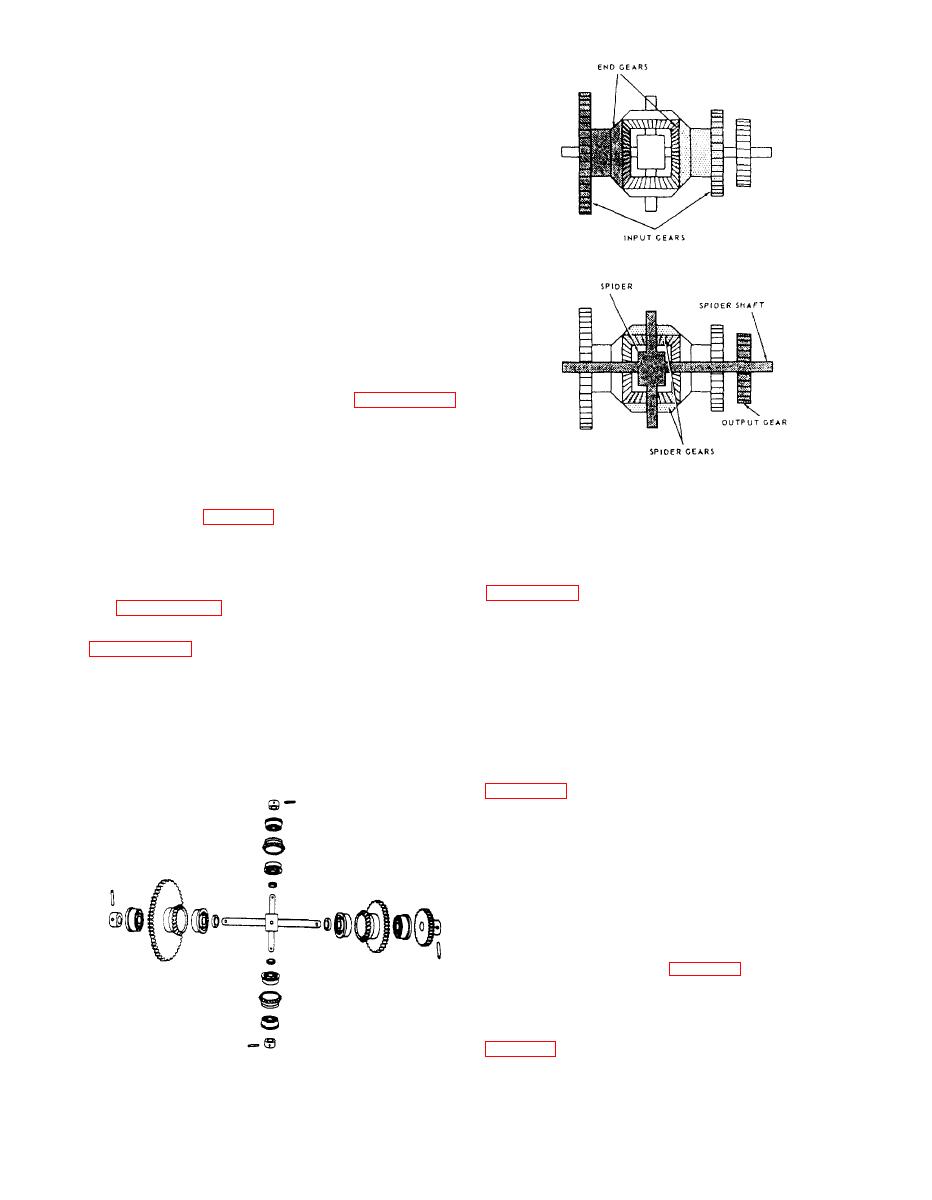two bevel gears above and below are called spider

gears. The long shaft running through the end gears

and the three spur gears is called the spider shaft. The

short shaft running through the spider gears, together

with the spider gears themselves, is called the spider.

Each of the spider gears and the end gears are

bearing mounted on their shafts and are free to rotate.

The spider shaft is rigidly connected with the spider

cross shaft at the center block where they intersect.

The ends of the spider shaft are secured in flanges or

hangers, but they are bearing mounted and the shaft is

free to rotate on its axis. It follows then that to rotate

the spider shaft, the spider, consisting of the spider

cross shaft and the spider gears, must tumble, or spin,

on the axis of the spider shaft, inasmuch as the two

shafts are rigidly connected.

The three spur gears shown in figure 10-25

connect the two end gears and the spider shaft to other

mechanisms. They may be of any convenient size.

Each of the two input spur gears is attached to an end

gear. An input gear and an end gear together are called

Figure 10-27.--End gears and spider arrangement of a

differential.

a side of a differential. The third gear is the output gear

(as designated in fig. 10-25). This is the only gear that

is pinned to the spider shaft. All of the other gears,

output. Later, it will be shown that any of these three

both bevel and spur, in the differential are bearing

gears can be either an input or an output. Now, look at

mounted.

figure 10-28. In this hookup, the two end gears are

Figure 10-26 is an exploded view of a gear

positioned by the input shafts, which represent the

differential showing each of its individual parts, and

quantities to be added or subtracted. The spider gears

figure 10-27 is a schematic sketch showing the

do the actual adding and subtracting. They follow the

relationship of the principle parts.

rotation of the two end gears, turning the spider shaft

a number of revolutions proportional to the sum, or

For the present, we will assume that the two sides

difference, of the revolutions of the end gears.

are the inputs, and the gear on the spider shaft is the

Suppose the left side of the differential is rotated

while the other remains stationary (as in block 2 of

fig. 10-28). The moving end gear will drive the

spider gears, making them roll on the stationary

right end gear. This motion will turn the spider in

the same direction as the input and, through the

spider shaft and output gear, the output shaft. The

output shaft will turn a number of revolutions

proportional to the input.

If the right side is now rotated and the left side held

stationary (as in block 3 of fig. 10-28), the same thing

will happen. If both input sides of the differential are

turned in the same direction at the same time, the

spider will be turned by both at once (as in block 4 of

fig. 10-28). The output will be proportional to the sum

of the two inputs. Actually, the spider makes only half

Figure 10-26.--Exploded view of a differential gear system.

10-14